Define mean absolute deviation

Mean’ refers to the average of the observations and deviation implies departure or variation from a preset standard. When put together, we can define mean deviation as the mean distance of each observation from the mean of the data. Absolute deviation synonyms, Absolute deviation pronunciation, Absolute deviation translation, English dictionary definition of Absolute deviation. In a statistical distribution or a set of data, the average of the absolute values of the differences between individual numbers and their mean.

The first application is that this statistic may be used to teach some of the ideas behind the standard deviation. Mean absolute deviation (MAD) of a data set is the average distance between each data value and the mean. Mean deviation definition is - the mean of the absolute values of the numerical differences between the numbers of a set (such as statistical data) and their mean or median. See the full definition.

Mean deviation definition, a measure of dispersion, computed by taking the arithmetic mean of the absolute values of the deviations of the functional values from some central value, usually the mean or median. It is a summary statistic of statistical dispersion or variability. The average of these numbers (÷ 5) is 1. Meaning of ABSOLUTE DEVIATION. What does ABSOLUTE DEVIATION mean ? Information and translations of ABSOLUTE DEVIATION in the most comprehensive dictionary definitions resource on the web. Define mean absolute deviation ? The total dollar amounts of the last orders are listed in the table below.

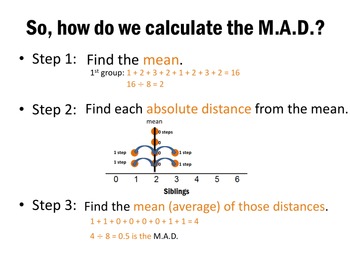
What is the mean absolute deviation of the data? To find the mean absolute deviation of the data, start by finding the mean of the. It is expressed by the following formula. Try to calculate the mean of the number of bubbles blown. And then, after you do that, see if you can calculate the mean absolute deviation.

The absolute value is used to avoid deviations with opposite signs cancelling each other out. Also called mean absolute deviation, it is used as a measure of. This calculator uses the following formula for calculating the mean absolute. Deviation definition, the act of deviating. Calculate the mean absolute deviation both with and without the data value of 55.

Round to the nearest hundredth if necessary. Explain how including the value of affects the mean absolute deviation. Explain why the mean absolute deviation is calculated using REASONING absolute value. Also known as mean absolute deviation.

It is a measure of dispersion when the number of values or quantities is small, otherwise use standard deviation. While there are many different ways to measure variability within a set of data, two of the most popular are standard deviation and average deviation , also called the mean absolute deviation. Compare the distribution of two data sets using mean absolute deviation. In working with data, there are several different ways to measure how closely grouped your data values are.

Most people learn early in school to. The most common is the mean. Some examples of specific topics discussed in the included papers are: benchmarking the operating efficiency of US airlines, cooperative public service advertising strategies for a supply chain system, multi-criteria performance measurement for public and private sector enterprises, and a meta-goal programming model for asset allocation of mutual funds under the mean absolute deviation.

The formula is a variation of the mean absolute deviation formula (see the mean absolute deviation article for more help in solving the formula). It is less affected by outliers because outliers have a smaller effect on the median than they do on the mean. In statistics, the mean absolute deviation is the mean of the absolute deviations of a set of data about the data’s mean. Calculates the mean absolute deviation from a center point, typically the sample mean or the median.

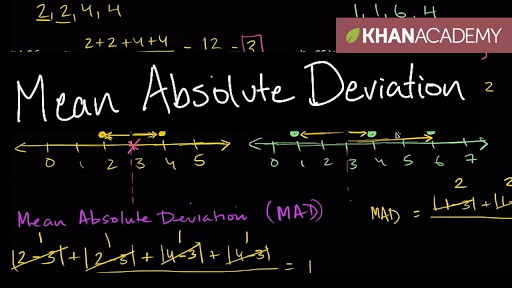
It is also termed as mean deviation or average absolute deviation. It can be calculated by finding the mean of the values first and then find the difference between each value and the mean. Take the absolute value of each difference and find the mean of the difference, which is termed as MAD.

Find the MAD of a data set using this mean absolute. In Section we review the main properties of the mean absolute deviation , and in Section basic on the sampling distribution of d , the sample mean absolute deviation about the sample mean , are presente together with a comparative study on the advantages in using S,,, and ,.